A Latent Variable Approach for Non-Hierarchical Multi-Fidelity Adaptive Sampling

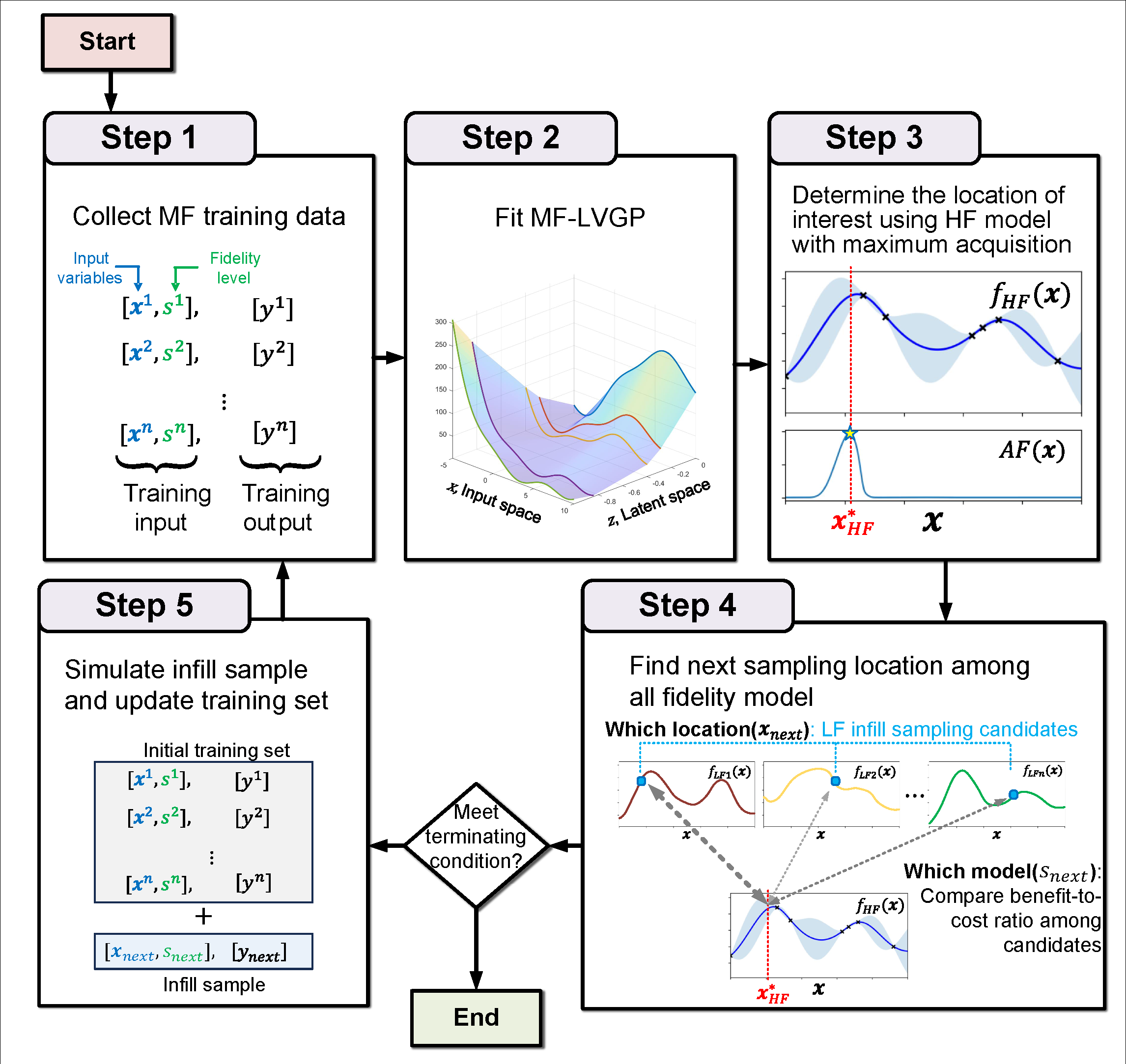
We propose an MF adaptive sampling framework hinged on a latent embedding for different fidelity models and an associated pre-posterior analysis to explicitly utilize their correlations to quantify the benefit of the candidate samples as the sampling criteria. In this framework, each infill sampling iteration includes two steps: First, we identify the HF location of interest with the greatest potential improvement of the high-fidelity (HF) model, and then search for the next sample across all fidelity levels that maximizes the improvement per unit cost at the location identified in the first step. This is made possible by a single Latent Variable Gaussian Process (LVGP) model that maps different fidelity models into an interpretable latent space to capture their correlations without assuming any hierarchy between fidelity levels. The LVGP enables us to assess how LF sampling candidates will affect HF response with a pre-posterior analysis and determine the next sample with the best benefit-to-cost ratio. Furthermore, the proposed method offers the flexibility to switch between global fitting (GF) and Bayesian Optimization (BO) by simply changing the acquisition function. Through test cases, we demonstrate that our method outperforms state-of-the-art methods in both MF GF and BO problems in the rate of convergence and robustness.

Keywords: Multi-Fidelity, Gaussian Process, Latent Variable, Adaptive Sampling, Active Learning, Pre-Posterior Analysis, Global Modeling, Bayesian Optimization, Benefit-aware

Recommended citation: Chen, Y. P., Wang, L., Comlek, Y., & Chen, W., "A Latent Variable Approach for Non-Hierarchical Multi-Fidelity Adaptive Sampling." Computer Methods in Applied Mechanics and Engineering, 421 (2024), 116773.
Download Paper